在线客服
2023-02-18 08:27 自考365
2023年4月自考备考已经开始，自考历年试题对考生来说是十分宝贵的资料，考前每道历年试题至少要做1-2遍才会事半功倍。自考365网给大家整理了2022年10月自考《线性代数（经管类）》试题及答案，一起来试试吧！
扫码入群>>获取自考公共课试题及答案
2022年10月高等教育自学考试全国统一命题考试线性代数（经管类）试题及答案
（课程代码 04184）
说明：在本卷中，AT表示矩阵A的转置矩阵，A*表示矩阵A的伴随矩阵，E是单位矩阵，|A|表示方阵A的行列式，r(A)表示矩阵A的秩。
一、单项选择题：本大题共5小题，每小题2分，共10分。在每小题列出的备选项中只有一项是最符合题目要求的，请将其选出。
1.已知3阶行列式D第1行的元素依次为1,2,-1，它们的余子式依次为2,-2,1，则D=
2.设A为3阶矩阵，P=
，则用Р右乘A，相当于将A
3.向量组α1=( 1,1,0 )T , α2=( 3,0,-9 )T ,α3=(1,2,3)T，α4=(1,-1,-6)T的秩是
4.设线性方程组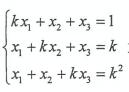
无解，则数k =
5.设矩阵A=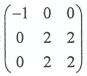
，则二次型f(x1,x2,x3)=xTAx的规范形为
二、填空题：本大题共10小题，每小题2分，共20分。
8.设A为3阶可逆矩阵，且|A|=2，则|-A*|=________
9.若矩阵A中有一个2阶子式不为零，且所有3阶子式均为零，则r(A)=________
10.已知向量组α1=(1,k ,-3 )T，α2=(3，6，-9)T线性相关，则数k =________
11.已知R2中的两组基：α1=(0,1)T，α2=(1,0)T和β1=(3,1)T，β2=(4,2)T，若矩阵Р满足(β1，β2)=(α1，α2)P，则P=________
12.设齐次线性方程组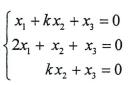
有非零解，则数k应满足的条件是________
13.设A为n阶可逆矩阵，且满足|2A-E|=0，则A-1必有一个特征值为________
14.设3阶矩阵A的特征值为1,-1,2，则|A2+2E|=________
15.若二次型f(x1,x2,x3)=x12+ax22+(a-2)x32+4x1x2正定，则数α应满足的条件是________
三、计算题：本大题共7小题，每小题9分，共63分。
16.已知行列式D=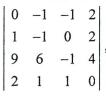
，Aij为元素aij的代数余子式，求A31-2A32+A33.
18.已知A=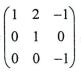
，B=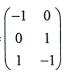
.(1）求A-1；(2）解矩阵方程AX = B.
20.设非齐次线性方程组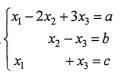
(其中a,b,c不全为零的常数)，当a,b,c满足什么条件时，方程组有无穷多解？并求其通解（要求用它的一个特解和导出组的基础解系表示).
22.求正交变换x=Py，将二次型f(x1,x2,x3)=x12+3x22+3x32-4x2x3化为标准型.
四、证明题：本题7分。
23.设向量组α1,α2,α3,α4线性无关，证明：向量组α1+c1α4，α2+c2α4，α3+c3α4线性无关（其中c1,c2,c3是任意常数）.
自考365提供从报名到毕业一站式服务！【点击咨询>> 】
=-2，则
=________
=________
，P=
，求A2.
，判定A是否可以相似对角化？并说明理由.
