本章重难点与考点分析
　　重点：
　　1.向量的各种运算
　　2.平面、直线、柱面、旋转面及一些常见二次曲面的标准方程及其图形
　　难点：
　　1.向量的运算
　　2.空间曲线在坐标面上的投影
　　考点：选择题、计算题，分值在10分左右

　　学习目标：
　　本章内容既是学习多元微积分的预备知识，同时其自身也是十分重要的数学工具，在很多后续课程中有广泛应用.由于向量的表示、运算及处理方法与数量有很大区别，初学者比较生疏，而掌握空间图形也要求有较强的空间想象能力，这都给初学者带来一定困难，因此自学时要注意掌握重点，多做习题.特别要掌握运用向量建立平面、直线方程的方法，以及常用的曲面、曲线的方程和图形，这是学习后续内容必需的基本知识.

　　
第一节　空间直角坐标系
　　知识点1　空间直角坐标系的建立
　　三维空间中几何问题
　　空间图形形式—点，线，面，体
　　
　　代数理论表达—坐标，方程（组）

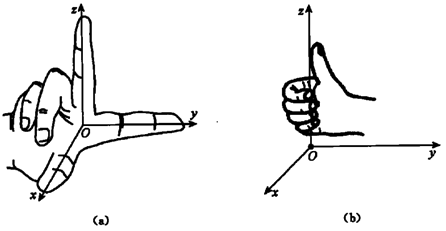
　　经过空间定点O作三条互相垂直的数轴，它们都以点O为原点，具有相同的单位长度.这三条数轴分别称为x轴（横轴）、y轴（纵轴）、z轴（竖轴），统称为坐标轴，并且各坐标轴正向之间的顺序要求符合右手法则，即以右手的拇指对准x轴的正向，食指对准y轴的正向，顺势伸出中指，此时中指的指向与z轴的正向一致；或者以右手握住z轴，让除大拇指外的四指从x轴的正向以90°的角度转向y轴的正向，这时大拇指所指的方向就是z轴的正向.这样组合的三条坐标轴构成一个空间直角坐标系.
　　

　　
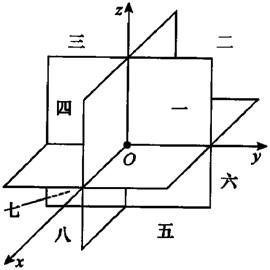
　　知识点2　空间直角坐标系的定义
　　定义1　三条坐标轴中的任意两条都可以确定一个平面，称为坐标面，它们是由x轴及y轴所确定的平面Oxy平面；由y轴及z轴所确定的Oyz平面；由x轴及z轴所确定的Ozx平面.这三个相互垂直的坐标面把空间分成八部分，每一部分称为一个卦限.位于x轴、y轴、z轴正半轴的卦限称为第一卦限，从第一卦限开始，在Oxy平面上方的卦限，按逆时针方向依次称为第二、三、四卦限；第一、二、三、四卦限下方的卦限依次称为第五、六、七、八卦限.
　　

　　
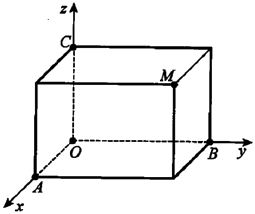
　　知识点3　空间点的坐标
　　定义2　在建立空间直角坐标系之后，对于空间中任意一点M，过点M分别作垂直于x轴、y轴、z轴的平面，它们与三条坐标轴分别相交于点A，B，C.设这三点在x轴、y轴、z轴上的坐标依次为x，y，z，则点M唯一确定了一组有序数x，y，z.这样，空间中的点M就可与一组有序数x，y，z之间建立一一对应关系.这时，有序数组x，y，z称为点M的坐标，记为M（x，y，z），其中x，y，z分别称为点M的横坐标、纵坐标、竖坐标.